となります 三角形の面積は,いろんな求め方がありますそこで, ヘロンの公式など を用いて三角形の面積を求めておくと,内接円の半径が求まります ヘロンの公式 三辺の長さが a , b , c である三角形の面積 S を求めるには まず、 s= abc2nnnnn を 球の表面積の求め方 半径rの円の面積はπr²で求める事ができますが、それでは球の表面積はどうやって求めればいいのでしょうか? ちなみに、「表面積」というのは立体の表面の面積のことを言います。なので、「球の表面積」とは言いますが「円の表面積」とは言いません。 球の表面積Page 3 内接球の半径 半径 ri は点o から ∆abc および ∆bcd を含む平面までの距離 より,oh hk, である. 6 3 dh a= ,do oh 31= 以上より, 1 6 i 4 12 r oh dh a= = = 辺に接する球の半径 半径 re は,辺da および辺bc m( ) までの距離より,on om, である.すなわち,mn は辺に接する球の直径ということに
1
球の半径の求め方 中学生
球の半径の求め方 中学生- 球の表面積の求め方公式 半径 r の球の表面積を S とすると、球の表面積 S は次の公式で求められます。 S = 4πr² (例題)半径が4cmの球の表面積を求めましょう。 求める球の表面積を S 、半径を r とすると、 S = 4πr² より S = 4π × 42 = 4π × 16 = 64π一部が欠けた球の体積 こういうサイトを探していました。 助かりました。 液体接触角の滴定量計測。 今まで表計算ソフトを使って手入力計算していましたが、偶然こちらのサイトを見つけました。 もっと早く見つければよかったです。 超音波




空間図形 内接球と外接球 Youtube
人類はどうやって球の体積を求めたのか 1、アルキメデスは球の体積をどうやって見つけたの? T:球の体積は半径をrとすると、4/3・π・r 3 で求めることができるんです。覚え方は、『3分で忘れる心配あーるの参上。』『身の上に心配あーるのさんじょう球の体積の考え方の例 -πr³ 球の表面積の考え方の例 4πr² 4 3 円がぴったり 入る円柱 円がぴったり 入る円柱 球の直径と等しい長さの半径をもつ円になった 円の面積=π(2r)² (rは球の半径) =4πr² 球の表面積=円柱の側面積→円柱の側面積を求める 具体物での実験をもとに公式を導き高校数学では習いませんが,三次元極座標(球座標)を用いて表現することもできます。 5.原点中心で半径が r r r であるような球面は,媒介変数 θ, ϕ \theta,\phi θ, ϕ (ただし, 0 ≤ θ ≤ π 0 ≤ ϕ < 2 π 0\leq \theta \leq \pi\0\leq\phi
中学生の勉強方法 中2数学1次関数による面積の求め方を解説! 中学生の勉強方法 123 中2数学連立方程式とは何だろう?その意味と解き方について解説します! 中学生の勉強方法 中学英語人称ってなに?単数・複数ってなに?(積分を使って計算していくと4倍になることがわかります。時間がある方は計算してみてください。) よって、半径をrとすると、球の表面積の式は、 になります。 3.球の体積を求める方法 球の体積は、小さな三角錐に近い形をしたものを足し合わせていくと求めることができます。 下の図 球の表面積の求め方には公式があるんだ。 球の半径をrとすると、その表面積は、 4πr^2 になるよ。 つまり、 4 × 円周率 × 半径 × 半径 ってわけだね。 たとえば、半径30cm のサッカーボールがあったとしよう。 このボールの皮の面積、つまり表面積は、 4 × π × 30
円の半径とは、円の中心から円周上の任意の点を結んだ線の長さです。 半径を最も簡単に求める方法は直径を2で割ることです。 直径がわからなくても、円周 ( C = 2 π r {\displaystyle C=2\pi r} )や円の面積 ( A = π r 2 {\displaystyle A=\pi r^ {2}} )など他の値が与えられ年で球の体積導出の方法を学ぶ授業(佐伯,1990, pp2735),錐体の体積公式を区分求積法の考えで導 き,その過程を球に活かして体積公式を導出する授業 (沖山, 06, pp), 半径1の 例題5)図1のように、高さが6cmで、底面の直径が高さと等しい円柱と、図2のように、半径3cmの球がある。図1の円柱の体積から、図2の球の体積をひいたときの差を求めなさい。 19 三重県公立高校入試問題 41



Q Tbn And9gctjav6gvj1k5jlr5jeyhgdtl 5v264jxhqxszqv9lgkyrvbr9tp Usqp Cau




いろいろ 球体 の 体積 公式
地図の下の方を見れば分かるとおり、たしかに南極大陸が無限にデカい。。 ということで、「球を平面で表現する」っていうのはめちゃめちゃ難しいんだね。 じゃあサイズ感を変えずに、平面で球を表現する場合、どんな図法があるだろう? 地球儀をみてみよう。 実は、()みたいな形に 円の半径=球の周の長さの 1 4 = 1 2πr 半径 1 2πr の円と見立てて面積を求めると, 面積= 1 2πr × 1 2πr × π = π2 4 πr2Scipursuit 体積の求め方 球 球の体積を求める公式は、次の通りです。 V = 4 3πr3 V = 4 3 π r 3 ここで、V は球の体積、r は球の半径、π は円周率を表します。 球の体積を求めるには、この公式に球の半径 r を代入すればよいだけです。 このページの続きでは




高校数学 正四面体 外接球の半径 オンライン無料塾 ターンナップ Youtube




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく
中学生でもおぼえられる「球の体積の求め方」 を解説していくよ。 球の体積の公式を忘れちゃったときに参考にしてみて。 球の体積の公式を1発で覚える方法 「球の体積の公式」を暗記する方法を伝授しよう。 3分の4 × 円周率 × 半径の三乗 中1 中1数学球の計算のポイント 中学生 数学のノート Clear 表紙 1 2 公開日時 19年04月25日 15時30分 更新日時 年08月02日 12時30分 中学生 1年生 数学接触球の半径は1ですから、2つの回転面の点Pにおける曲率Kはともに1です。 ちょっと見ると、双曲面の曲率の方が放物面の曲率より小さいように思えますが、そうではありません。 曲率は1点Pで見てのことですから。 この曲面は回転面ですので、その母線の曲率をFig1のように求めて2乗しても




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張




球の表面積の求め方 公式と計算例
最後に 球の体積 球の体積 目標:積分をつかって上式を導出する 2つの方法を考えました. 方法1:回転体として考える. 方法2:球体の表面積を使う. 方法1:回転体として考える 前提知識 原点中心,半径 の 円柱の体積の求め方=半径×半径×円周率×高さ 円柱に関して、体積を求める問題がよく作られます。たとえば上の写真のように、底の円の半径と円柱の高さが示されて「この円柱の体積を求めよ」と問われます。 上の情報を元に計算の流れを説明していきましょう。まずは底面積(S)を求め円すい(円錐)の体積の求め方と問題 図形の面積(体積)や周りの長さを文字式にする問題まとめ 補足 上の練習問題で、半径が2cmの球は半径が1cmの球に比べて、体積は8倍、表面積は4倍になっています。 半径が2倍になると、体積は8倍になる。




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張




中1 数学 中1 84 球について Youtube
球の体積と表面積 半径 r r の球の体積と表面積を求める公式は以下のようになります。 球の体積= 4 3 πr3 球 の 体 積 = 4 3 π r 3 球の表面積=4πr2 球 の 表 面 積 = 4 π r 2 r(a b c) の3次元バージョンです。 内接球の半径,表面積,体積のうち2つ分かれば残りの1つも分かる という公式ですが,ほとんどの場合表面積と体積から内接球の半径を求めることにな円すいの展開図 円すいの展開図は、下図のようになります。 側面を切り開いたおうぎ形と底面の円からなります。 側面のおうぎ形の中心角は、以下の公式から求めることができます。 円すいの側面の中心角= \(360×\)\(\d




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




内接球 外接球の求め方についてです 2枚目の赤で書いているところが理解出来ません Clear
もし、球の表面積の公式を忘れてしまった人は、昨日の球の表面積の求め方!中学生の子に公式の覚え方のコツを紹介! を確認してきてください。それでは問題です。 ・下の球について、 最初にも言ったように、球の「表面積」と「体積」の2つの公式を間違えないようにしましょう。表面球の表面積の公式の求め方について考察する前段階として、球の体積の公式の求め方を 考察しておこう。下の図1において、球の中心から距離 x の点で切った断面である円の半径は √(r 2 -x 2) であるから、円の面積は、S(x)=π(r 2 -x 2) となる。 よって、球の体積Vは、円の面積を x 方向に球の切り口の面積についてです⤵︎ ⤵︎ 辺ab,bc,cfの中点をそれぞれl,m,nとします。 立体s(3点acfを通る平面で切ったとき点bを含む方の立体)を3点lmnを通る平面で切ったとき sに内接する球の切り口の面積の求め方を教えてください!




球の半径を求める 3つの方法 Wikihow




中学 数学 テクニック 内接球の半径の求め方 高校入試 高校受験 裏ワザ Youtube
球の体積の求め方 それでは次の例題で、球の体積を求める練習をしましょう。 例題 次の球の体積を求めよ。 まず最初に、体積の公式を余白にでも書き出しておきましょう。 \(\displaystyle V = \frac{4}{3} \pi r^3\) 体積を求めるために必要な値は \(r\)(半径)だけですね。 問題の図を見ると高校生・数学3C 記事詳細 数学講師必見中学数学でも必須! 球の体積、表面積の覚え方と導出まとめ! 高校数学 31,704 views 14年06月21日公開 キーワード 球フェルミ球 一辺Lの立方体の箱に入った粒子の1粒子準位は ε(p) = 1 2m (p2 x p 2 y p 2 z) (21) = ¯h2 2m (k 2 x ky k 2 z) (22) である.ここで運動量と波数nx,ny,nz を整数として p = ¯hk = ¯h 2π L (nx,ny,nz) (23) で与えられる.nまたはkまたはpの空間での格子点がひとつの1




半径 求め 方 ニスヌーピー 壁紙
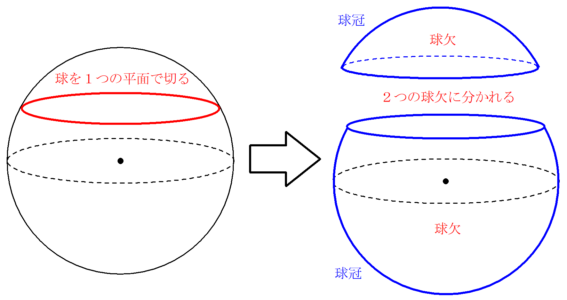



球欠と球冠 Fukusukeの数学めも
球の表面積 = 4 × 314 × 半径 × 半径21 球の体積(アルキメデスの求積) ここでは,アルキメデスによる球の体積の求め方について述べる. 力のモーメントを用います.力のモーメントといっても棹秤(さおばかり)の性質です. すなわち,棹ばかりの重さを無視すれば右図でつり合いがとれていればM号球は中学生以上の大会で、J号球は小学生の大会で使用されています。素材はゴム製。公式試合に使われる公認球は、硬さや縫い目の数などもすべて厳密に決められています。 硬式野球ボールのサイズ 硬式 目安 小学生 ~ プロ 直径 7293~7484mm 重さ 1417~14g 反発高さ 48~55cm プ




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




小学3年生の算数 円と球 練習問題プリント ちびむすドリル 小学生
実はこの考え方は三角錐によらず、あらゆる多面体に対して使うことができます。 これを一般的な公式として表したのが次の式です。 多面体の内接球の公式 V = 1 3rS V = 1 3 r S V V :多面体の体積 S S :多面体の表面積 r r :内接球の半径 ただし公式を丸
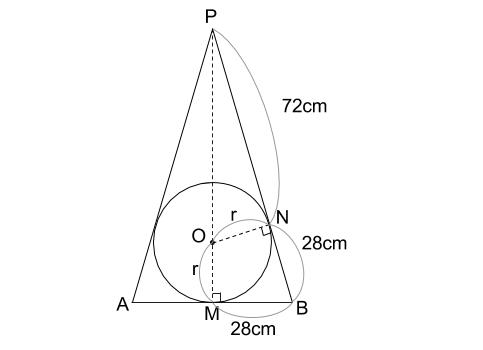



円錐と内接球 その1 中学数学の無料オンライン学習サイトchu Su




球の半径を求める 3つの方法 Wikihow




扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア




三角錐の内接球の半径の求め方を四角錐でも使うことが出来るのですか Clear




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




正四面体の公式まとめ 体積 高さ 内接球 外接球 重心 理系ラボ



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス
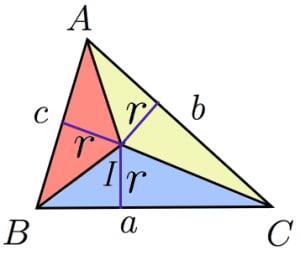



内接球の半径を求める一般的な公式 高校数学の美しい物語




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ
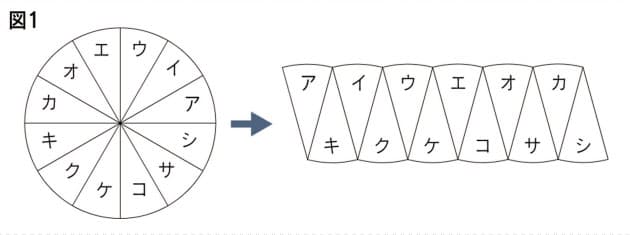



子供に説明できる 円の面積の公式 の証明 Nikkei Style
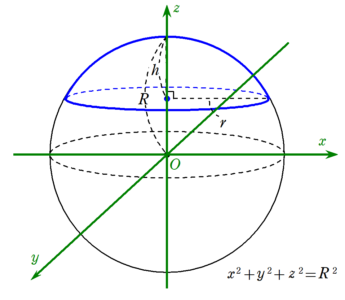



球欠と球冠 Fukusukeの数学めも




球の体積と表面積 公式と計算問題と証明 Irohabook




球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ
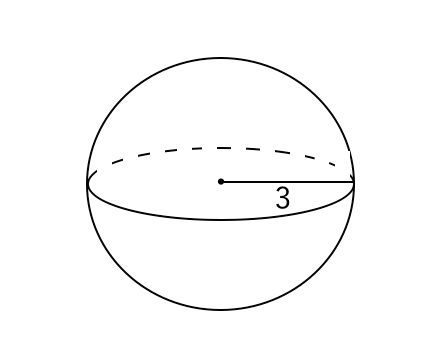



球の表面積と体積の求め方 苦手な数学を簡単に




円錐と内接球 その1 中学数学の無料オンライン学習サイトchu Su




正四面体の公式まとめ 体積 高さ 内接球 外接球 重心 理系ラボ
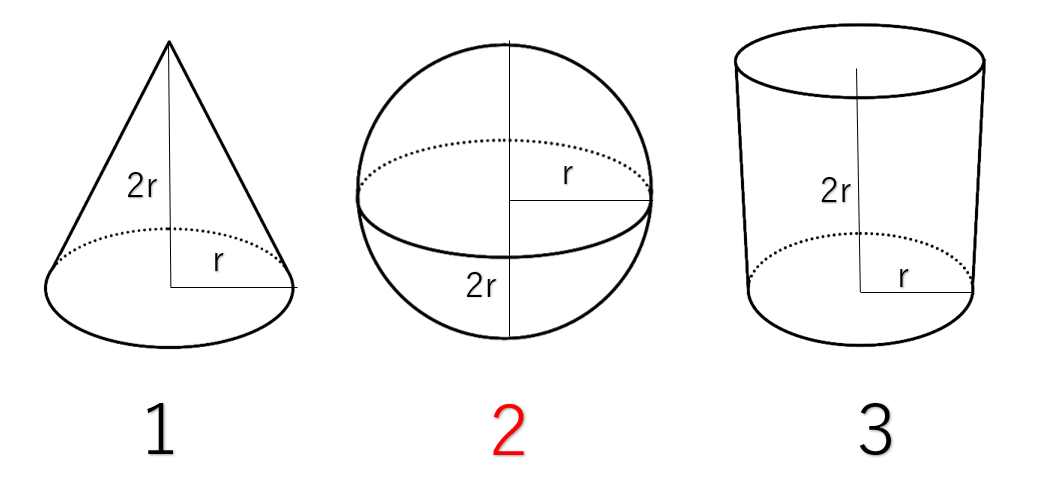



中1 数学 暗記に頼らない 球の体積の求め方 こいがくぼ翼学習塾




球の表面積と体積の公式 数学fun




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




円 扇形 の面積 周や弧の長さの公式 数学fun
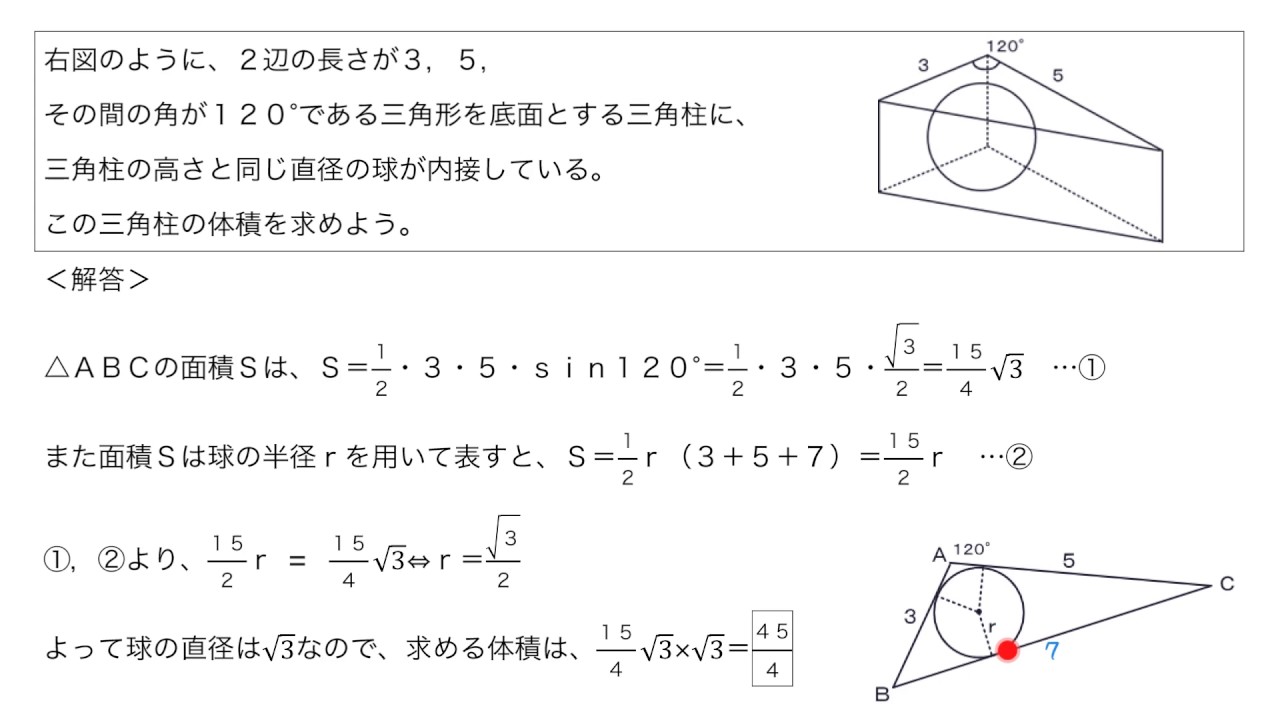



例題 三角柱に内接する球 Youtube




球の表面積と体積の公式 数学fun




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




球の半径を求める 3つの方法 Wikihow



半径5cmの球の表面積と体積を求めよ 教えてください Yahoo 知恵袋




球の体積と表面積 公式と計算問題と証明 Irohabook




中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス
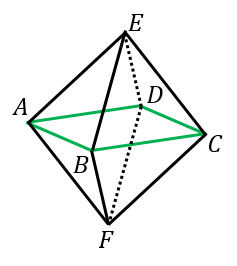



正八面体の体積 表面積 外接球の半径 内接球の半径 具体例で学ぶ数学



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




内接球の半径を求める一般的な公式 高校数学の美しい物語




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
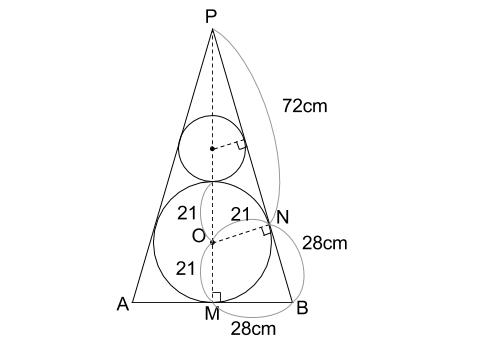



円錐と内接球 その2 中学数学の無料オンライン学習サイトchu Su




角錐 円錐の体積と表面積の公式 数学fun



1




三角比50 外接球の半径 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学b 球面の方程式 1 練習編 映像授業のtry It トライイット



1




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




円周の求め方 公式は直径を使うので 半径と間違えないように 中学や高校の数学の計算問題



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス




高校数学 正四面体の計量 表面積 2面のなす角 高さ 体積 内接球の半径 外接球の半径と立方体への埋め込み 受験の月



Math 高校入試の難問 内接する球 外接する球 働きアリ The 2nd
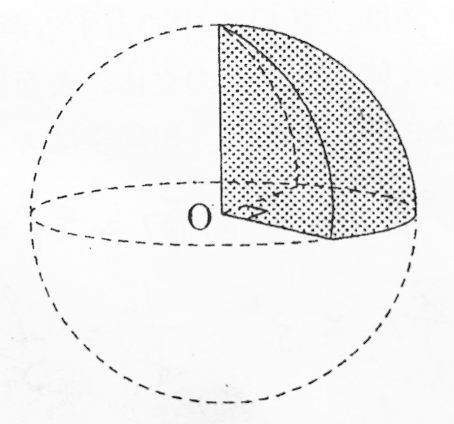



球の問題 苦手な数学を簡単に



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ



内接球の半径を求め方が分かりません 解説お願いします 直角が1つの頂点に Yahoo 知恵袋




円周の求め方 公式と計算例



正四面体とは 高さ 体積 表面積の公式や求め方 受験辞典



円の面積 円周の求め方 公式 小学生 中学生の勉強




球の体積の求め方 公式の覚え方と計算方法まとめ 中学数学 理科の学習まとめサイト




球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題




空間図形 内接球と外接球 Youtube




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




三角錐の内接球の半径の求め方を四角錐でも使うことが出来るのですか Clear



2




球の体積 表面積 中学生にも納得のいく方法で 積分でも出します Youtube




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




球の表面積と体積の公式 数学fun
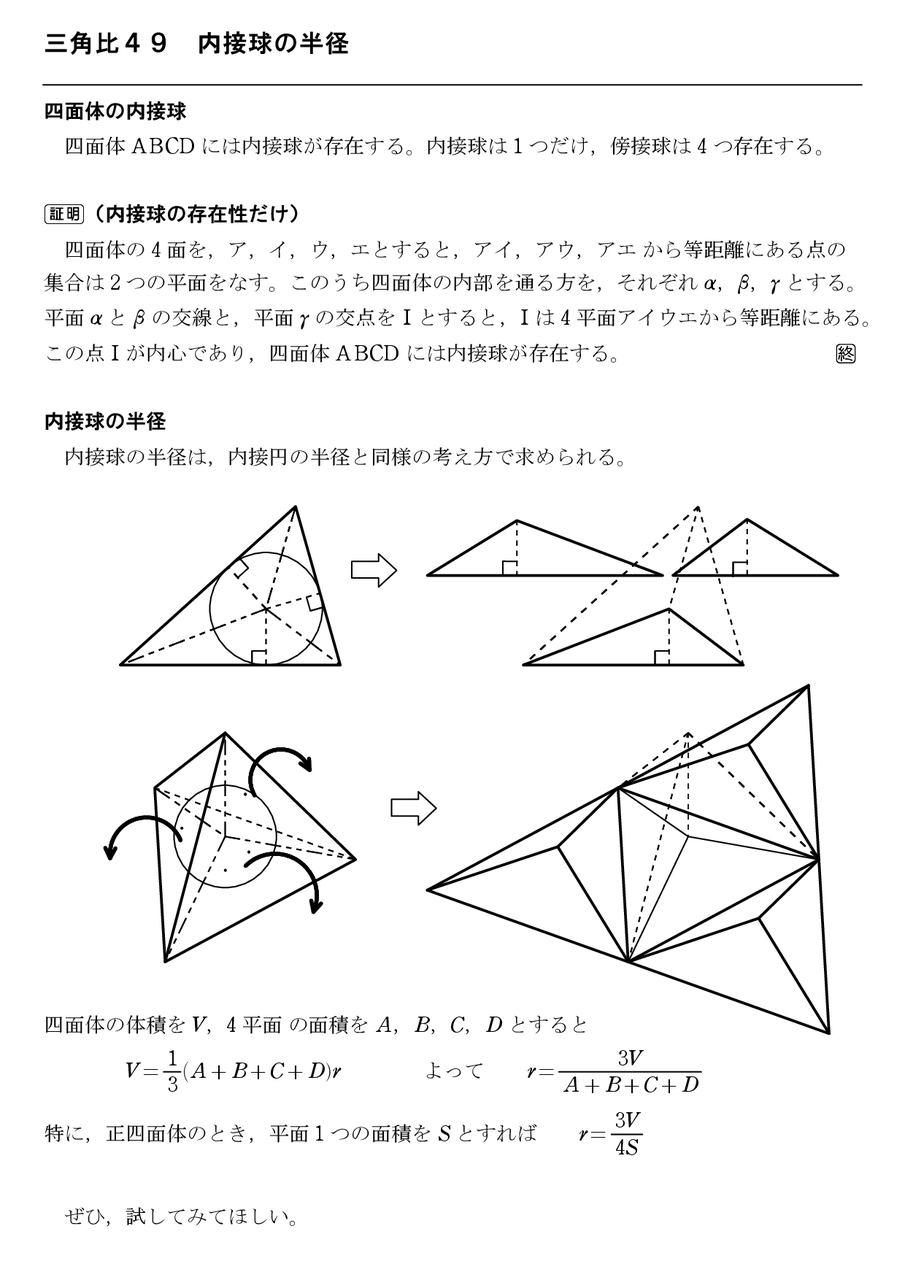



三角比49 内接球の半径 怜悧玲瓏 高校数学を天空から俯瞰する




球の表面積と体積の公式 数学fun




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく




球の半径を求める 3つの方法 Wikihow




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学



三角錐に内接する球の半径の求め方 こんにちは中学三年ですが Yahoo 知恵袋



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス
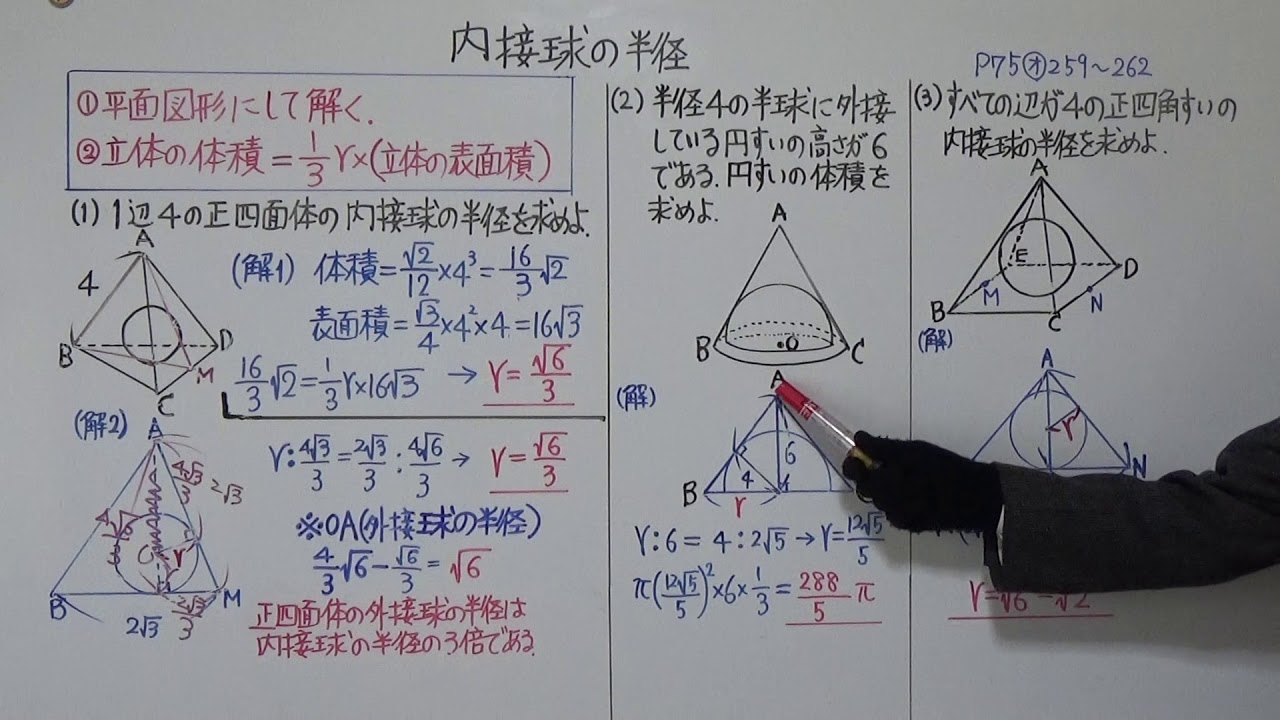



58 内接球の半径 Youtube



正四面体とは 高さ 体積 表面積の公式や求め方 受験辞典



円錐の底面の半径が3 母線の長さが6です この球の半径の求め方 Yahoo 知恵袋




球の表面積と体積の公式 数学fun




球の半径を求める 3つの方法 Wikihow



球の体積 簡単に計算できる電卓サイト




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




三角錐の内接球の半径の求め方を四角錐でも使うことが出来るのですか Clear




半球の体積と表面積を計算する 具体例で学ぶ数学



1




中1 数学 6 5 球の体積 表面積 Youtube




正四面体の公式まとめ 体積 高さ 内接球 外接球 重心 理系ラボ



下の円すいの底面の半径の求め方どうやって 求めれば良いのですか Yahoo 知恵袋




球の体積 表面積 実験から公式を 授業実践記録 アーカイブ一覧 数学 高等学校 知が啓く 教科書の啓林館




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿